BackdoorCTF 2025 - m4c&ch3353
Prove that you have enough power to climb the tower snatch the partially broken treasure and fix it!
chall.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
import math
from Crypto.Hash import CMAC
from Crypto.Util.number import long_to_bytes, getPrime, bytes_to_long, isPrime
from Crypto.Cipher import AES
from hidden import power_tower_mod, flag
assert bytes_to_long(flag).bit_length() == 1263
"""
power_tower_mod -> takes x, n and some data and returns
.
.
.
x
x
x
x
x mod n
i.e. infinite power tower of x modulo n
x^(x^(x^(x^(x.......))))) mod n
There are no vulnerabilities in that function trust me!!
"""
class bigMac:
def __init__(self, security = 1024):
self.security = security
self.n, self.data = self.generator()
self.base = getPrime(security) * getPrime(security)
self.message = bytes_to_long(flag)
self.process()
self.verified = False
self.bits = 96
self.keys = []
for i in range(self.bits):
self.keys.append(getPrime(self.bits))
print("My m4c&ch3353:", self.mac)
print("My signature: ", self.getSignature(self.base))
self.next()
def generator(self):
chunk = 128
while 1:
data = []
n = 1
for i in range(2 * self.security // chunk):
data.append([getPrime(chunk), 1])
n *= data[-1][0]
data.append([2, 2 * self.security - n.bit_length()])
while n.bit_length() < 2 * self.security:
n *= 2
if n.bit_length() == 2 * self.security:
return n, data
def process(self):
x = long_to_bytes(self.n)
cc = CMAC.new(x[:16], ciphermod=AES)
self.mac = cc.update(x).hexdigest()
def getSignature(self, toSign):
return (toSign * toSign) % (1 << (toSign.bit_length() - (self.security // 250)))
def verify(self, N, data):
self.next()
if self.verified:
print("ALREADY VERIFIED")
return False
if N.bit_length() != 2 * self.security:
print("size of N is not correct.")
return False
prev = self.n
mac = self.mac
self.n = N
self.process()
x = 1
maxPrime = 0
for i in range(len(data)):
data[i][0] = int(data[i][0])
data[i][1] = int(data[i][1])
if not isPrime(data[i][0]):
self.n = prev
self.mac = mac
print("Gimme primesssssss onlyyyy!!")
return False
x *= pow(data[i][0], data[i][1])
maxPrime = max(maxPrime, data[i][0])
if self.mac != mac or x != N or maxPrime.bit_length() > self.security // 5:
self.n = prev
self.mac = mac
print("Failed to verify.")
return False
print("Yayyyyyyyy! big mac got verified! for n =", prev)
print("Data =", self.data)
self.data = data
self.n = N
self.verified = True
return True
def next(self):
self.base = power_tower_mod(self.base, self.data, self.n)
def obfuscateSmall(self, m):
obs = m & ((1 << self.bits) - 1)
m ^= obs
final = 0
for i in range(self.bits):
if ((obs >> i) & 1):
final += self.keys[i]
return m + final
def communicate(self):
self.next()
if self.verified:
x = self.obfuscateSmall(bytes_to_long(flag))
while math.gcd(x, n) != 1:
x += 1
while math.gcd(self.base, self.n) != 1:
self.base += 1
print(f"Here is your obfuscated c: {pow(x, self.base, self.n)}")
else:
print("Verification needed.")
def power_tower(self, x):
self.next()
if self.verified:
print("WTF(What a Freak), you have n do it yourself.")
return -1
return power_tower_mod(x, self.data, self.n)
if __name__ == "__main__":
big = bigMac()
steps = 90
while steps > 0:
print("1: Communicate.")
print("2: Verify.")
print("3: Obfuscating.")
print("4: Quit.")
steps -= 1
x = int(input("Choose: "))
if x == 1:
big.communicate()
elif x == 2:
n = int(input("Give me the MY modulus : "))
*inp, = input("Enter prime factorization in format [prime1, count1]-[prime2, count2]-[...: ").split('-')
data = []
for i in inp:
curr = i[1:-1].split(", ")
data.append([int(curr[0]), int(curr[1])])
big.verify(n, data)
elif x == 3:
x = int(input("Enter your message : "))
print("Here is your obfuscated message : ", big.obfuscateSmall(x))
elif x == 4:
print("Goodbye.")
quit()
else:
print("Wrong input.")
Understanding the challenge
We have three main functions:
- Communicate
- Verify
- Obfuscating
Let me go through what each of them do in brief.
1. Communicate
- This function can only be called once the verify check is passed once.
- The flag is obfuscated with option 3.
- Then it is encrypted with an RSA style encryption with
e=self.baseandN=self.Nwhich I will get back to later.
2. Verify
- We are asked to enter a number N and its prime factorization such that the following criteria is met:
- N is a 2048 bit number.
- Each factor of N must be less than or equal to 204 bits.
- The CMAC of our N must match with
self.N(We have to collide the CMAC)
- Once this criteria is met,
self.Nis replaced with our new N, additionally we get to know the originalself.Nand its factors.
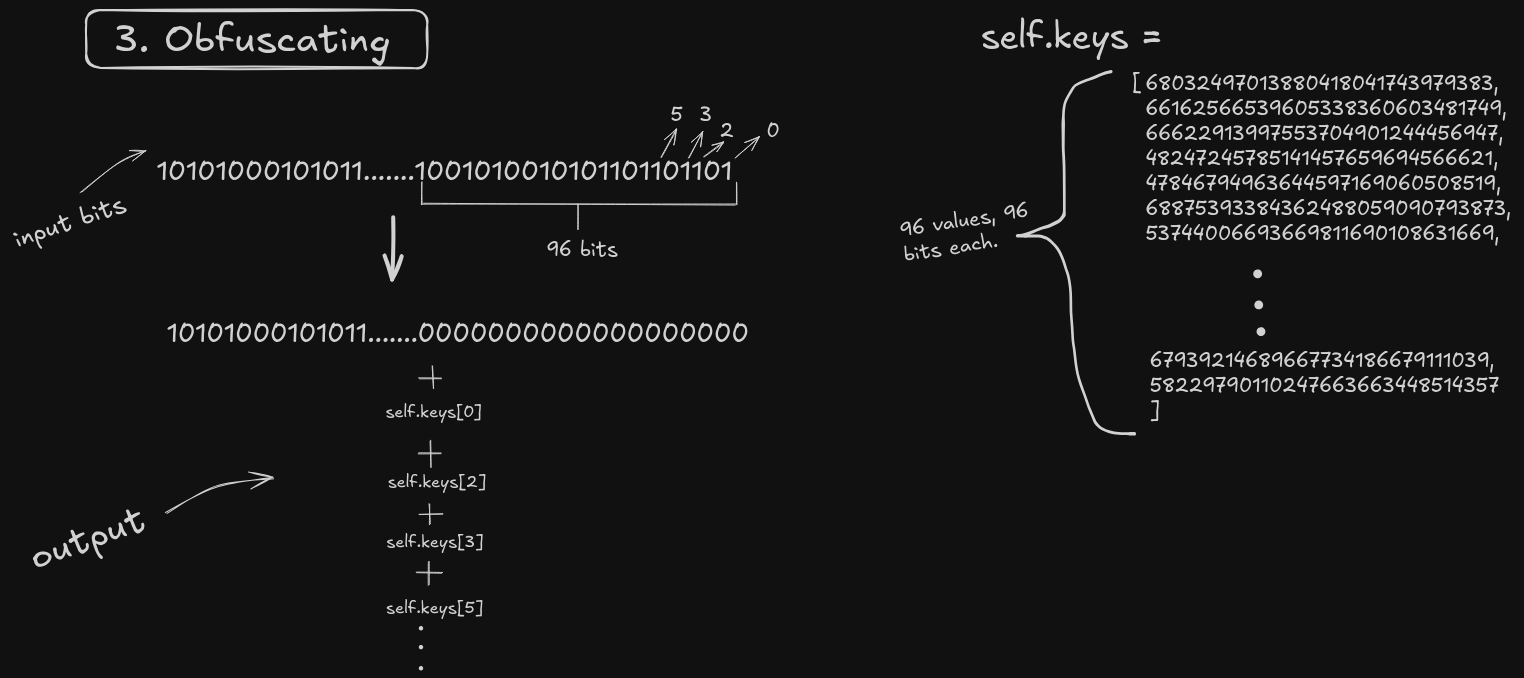
3. Obfuscating
1
2
3
4
5
6
7
8
9
def obfuscateSmall(self, m):
obs = m & ((1 << self.bits) - 1)
m ^= obs
final = 0
for i in range(self.bits):
if ((obs >> i) & 1):
final += self.keys[i]
return m + final
- This function takes in a number as input, and sets the LSB 96 bits to 0.
- The cut off 96 bits are iterated over (from lsb to msb), if a bit is 1, the corresponding value in
self.keysis added to our input.self.keysis a list of 96 numbers that are 96 bits each. - The final result is our obfuscated output.
There are a lot of intricacies involved in this challenge, I’ll discuss them now:
- We have just 90 total queries that we can call to any of the above functions.
power_tower_mod() and self.next() function
1 2
def next(self): self.base = power_tower_mod(self.base, self.data, self.n)
- The power_tower_mod function calculates the result of self.base raised to itself infinitely many times like a tower, modulo N. This function is hidden from us.
- The self.next() function is called before every communicate and obfuscate function calls as well as in the init function in the bigMac class.
- self.base is initially a 2048 bit number composed of two 1024 bit primes.
- self.N is a 2048 bit number composed of 16 primes of 128 bit length each.
- self.data is the factorization of
self.N
Solve approach
- Verify our N, by colliding the CMAC.
- Recover self.base which is the exponent.
- Recover all necessary keys using the obfuscate function.
- Run the communicate function and get the RSA ciphertext – decrypt by calculating phi given that the N used is the same N used to verify.
- Deobfuscate the flag by solving the subset sum problem on the last 12 bytes.
We have the flag!
How do we get self.base?
- We need self.base as well us self.N and its factors to decrypt the RSA ciphertext from the communicate method.
- Verify allow us to replace self.N with our own input.
This is where the getSignature() function comes in!
self.__init__()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class bigMac:
def __init__(self, security = 1024):
self.security = security
self.n, self.data = self.generator()
self.base = getPrime(security) * getPrime(security)
self.message = bytes_to_long(flag)
self.process()
self.verified = False
self.bits = 96
self.keys = []
for i in range(self.bits):
self.keys.append(getPrime(self.bits))
print("My m4c&ch3353:", self.mac)
print("My signature: ", self.getSignature(self.base))
self.next()
We are provided with the initial self.base value’s ‘signature’ as well as the CMAC value of the initial value of self.N.
self.getSignature()
1
2
def getSignature(self, toSign):
return (toSign * toSign) % (1 << (toSign.bit_length() - (self.security // 250)))
Which translates to ${self.base}^2 \pmod{2^{2044}}$
So given the signature, it is quite easy to get self.base.
Recovering self.base:
Assume $r=self.base^2$ and $a=self.base$,
We start with the assertion that $r \equiv 1 \pmod 8$ and $a \equiv 1 \pmod 8$
With this, we can continue lifting the value of $a$ modulus higher powers of 2 given the knowledge of the value of $r \pmod {2^{i+1}}$
We can do so because with the addition of one extra bit in the modulus, we can get the solution by testing whether the next bit in $a$ is 0 or 1 and squaring it to see if it matches with $r$ under the same modulus.
 So we get $a \pmod {2^{4}}, a \pmod {2^{5}}, a \pmod {2^{6}}$
So we get $a \pmod {2^{4}}, a \pmod {2^{5}}, a \pmod {2^{6}}$
We continue this until we find $a \pmod{2^{2044}}$
We will be left with two solutions as $-a$ and $a$ are two valid quadratic residues of $r$.
But, these are not our final candidate values of $self.base$.
$self.base$ is 2048 bits and we only have their 2044 bit equivalents, we need to prefix all possible 4 bit combinations for both roots.
 This leaves us with 32 candidate $self.base$ values.
This leaves us with 32 candidate $self.base$ values.
Passing the verification check
We are given the CMAC value of self.N (stored in self.mac) at the very beginning.
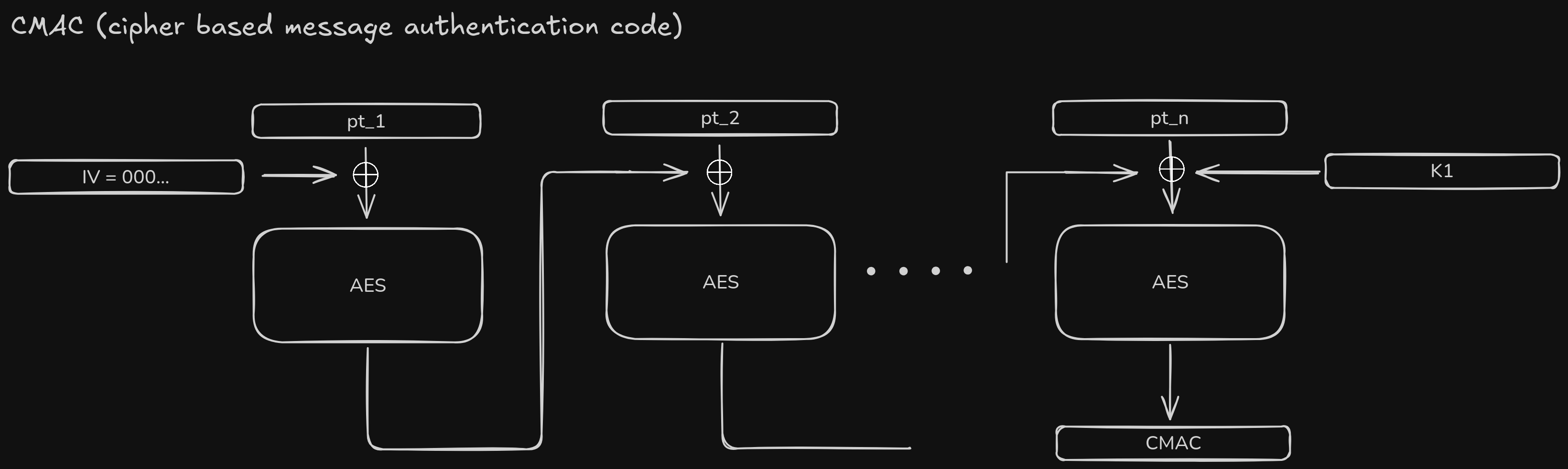
CMAC or Cipher based message authentication code is a type of MAC involving AES-CBC mode.
The MAC here is just the last block of your AES encrypted (under CBC mode) input with a small difference – the last plaintext block is XORed with the previous ciphertext as well as a derived key $K_1$ from the encryption key $K$.
Let $L = AES_k(0^{128})$
$K_1 = L \ll 1$ (if $msb(L)$ is 0)
$K_1 = (L \ll 1) \oplus 0x87$ (if $msb(L)$ is 1)
We have to input an N (and its factorization) which has the same CMAC value as the initial N. There is a fundamental flaw in the implementation of the CMAC function,
1
2
3
4
def process(self):
x = long_to_bytes(self.n)
cc = CMAC.new(x[:16], ciphermod=AES)
self.mac = cc.update(x).hexdigest()
The key is the first 16 bytes of our input.
The key is controlled by the user! and not by the server.
This changes the problem of colliding the CMAC with brute force, to colliding by using the properties of XOR.
Colliding the CMAC
- Our N must be 2048 bits long, this involving working with 16 blocks of plaintext in AES.
- What we can do is set the 14 blocks to all 0 bytes, the first block as random 16 bytes, and the $2^{nd}$ block as the repeated decryption of $dec_k(cmac_{N}) \oplus K_1$ (14 times) XORed with the first encrypted block.
Eventually, once the encryption and chaining happens with XOR like in standard AES, the last ciphertext block will be the same CMAC as the old N.
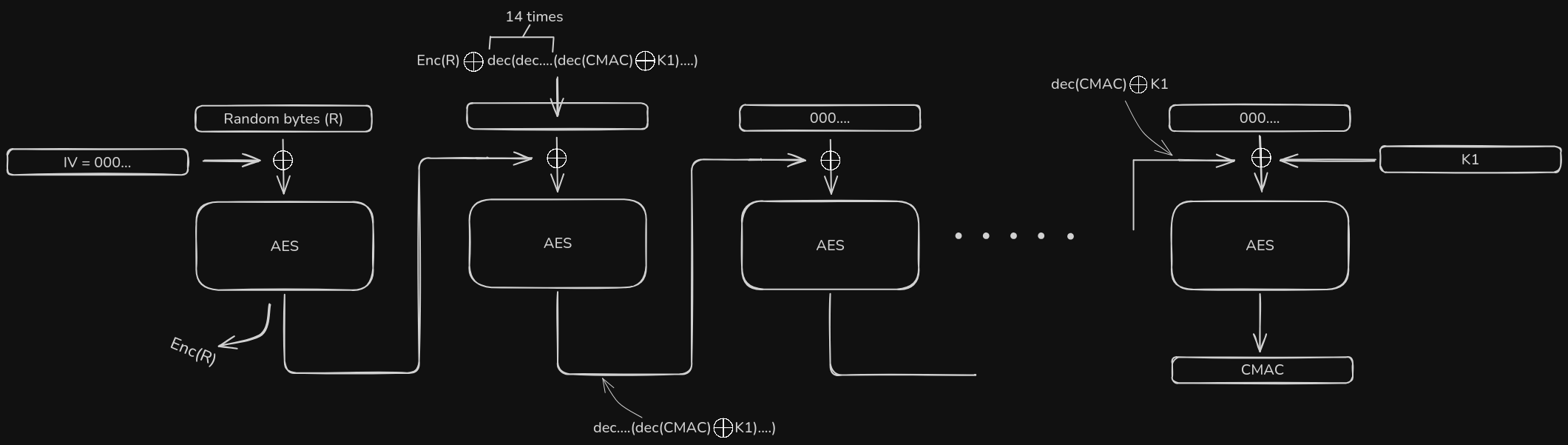
Factoring this number will be easy as it would be (in the worst case scenario) composed of a 256 bit prime and $2^{1792}$. This would be a rare scenario where the first two blocks form a prime. 90% of the time, the primes are always less than 204 bits, so we can proceed with verification.
self.N now becomes our new crafted N.
self.d is now our N’s factorization.
Recovering necessary keys.
- Our last step involves getting the RSA encrypted ciphertext, decrypting, then solving the subset sum problem on the obfuscated flag.
- We only have 90 total queries on all 3 functions combined, running the verify and communicate method once would bring it down to 88. And we have 96 total keys to recover.
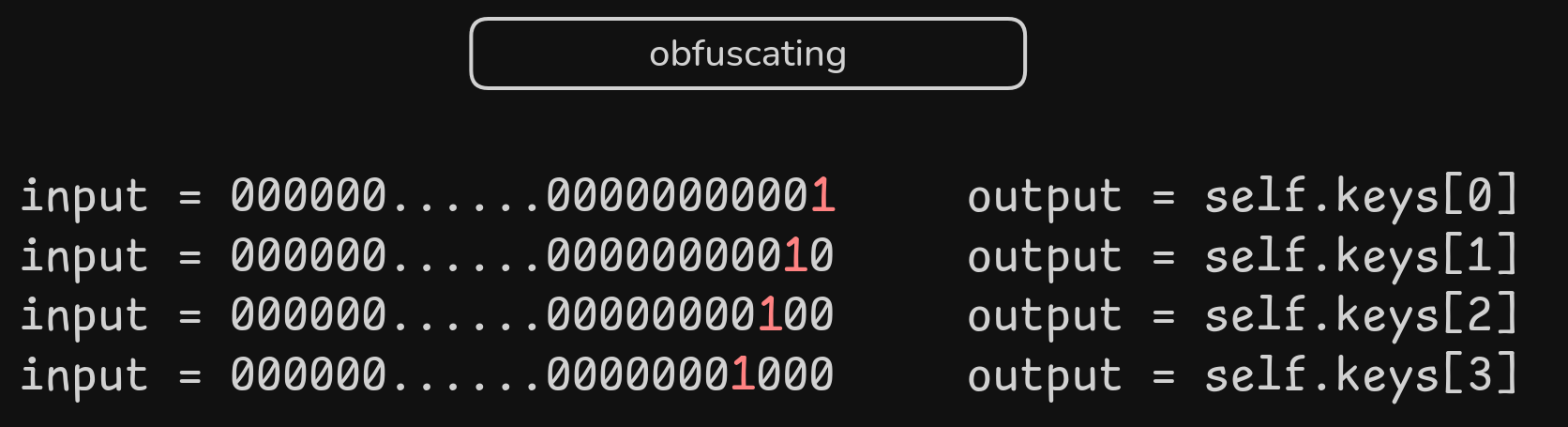
How do we recover all 96 keys with just 88 queries?
Tl;dr: We don’t have to.
We can use one query to get one key by passing $2^{i}$ to the obfuscate function to get the $i^{th}$ key in self.keys.
Optimization:
The MSB of each byte in the flag will be a 0 bit, as the range of numbers in the ascii table is 0 to 127 which can be represented with 7 bits. So we do not have to query for every 8th key in self.keys as they will never be used in the obfuscation of the flag.
So in total, we can reduce the number of keys needed from 96 to just 84!
(Additionally, we know that the last byte is } which corresponds to 01111101 in binary. We can send the equivalent of 11111111 = 255 to get the sum of all keys from indices 0 to 7 that will be used, further reducing the number of queries used.)
RSA decryption.
After recovering all necessary keys, the initial self.base value, the necessary keys that would have been used to obfuscate the flag, what’s left for us is to run the communicate function and get the obfuscated flag.
1
2
3
4
5
6
7
8
9
10
11
def communicate(self):
self.next()
if self.verified:
x = self.obfuscateSmall(bytes_to_long(flag))
while math.gcd(x, n) != 1:
x += 1
while math.gcd(self.base, self.n) != 1:
self.base += 1
print(f"Here is your obfuscated c: {pow(x, self.base, self.n)}")
else:
print("Verification needed.")
We have:
$x =$ obfuscated flag.
$c = x^{self.base} \pmod{self.n}$
We have the initial value of self.base, which we have recovered from the signature given at the very start.
But the self.next() function is run thrice until we get $c$.
Let’s recall that the function replaces self.base with power_tower_mod(self.base, self.data, self.n) and replaces self.base.
This changes the value of self.base.
- First,
self.next()is run at the end of the__init__(self)function. - Secondly,
self.next()is run at the very beginning ofverify(self, N, data). - Lastly, it is run at the very beginning of
communicate(self).
At the first two calls, self.n is the initial value of n generated by the code in __init__.
At the last call (since we called the verify function) our own value of n is used.
The power_tower_mod function is hidden
So we need to implement it ourselves.
 The fact that the function takes in the factorization of
The fact that the function takes in the factorization of self.n confirms the fact that the power tower is calculated as depicted above.
At each higher level, the exponentiation is done modulo $\phi({n})$ where $n$ is the modulus of the current level.
So at the $3^{rd}$ level, the exponentiation is done modulo $\phi(\phi({n}))$
The modulo will converge to 1 sooner or later.
Infact, it will converge with lesser than or equal to steps as the bit length of n. (it would take $i$ steps for the power_tower_mod function value to converge when $n=2^i$)
Let’s visualise this, with an example:
$N = 2^4 . 3^2 . 5^3$
$\phi(N) = 2^3.(2-1) . 3^1.(3-1) . 5^2.(5-1)$
$\phi(N) = 2^6 . 3^1. 5^2$
$\phi(\phi(N)) = 2^5.(2-1) . (3-1). 5(5-1)$
$\phi(\phi(N)) = 2^8.5$
$\phi(\phi(\phi(N))) = 2^7.(2-1).(5-1)$
$\phi(\phi(\phi(N))) = 2^9$
After 9 more operations, the value will converge to 1.
The bit length of $2^4 . 3^2 . 5^3 = 18000$ is 15 and 12 steps were required to converge the repeated $\phi$ to 1.
Bringing it together
Call the power_tower_mod functions thrice as follows:
1
2
3
4
b = #recover initial base from signature
b = power_tower_mod_optimized(b, old_factors, 2048)
b = power_tower_mod_optimized(b, old_factors, 2048)
b = power_tower_mod_optimized(b, new_factors, 2048)
Run the communicate function and get the obfuscated c. Then decrypt with RSA,
1
2
3
4
5
6
7
while gcd(b, new_N) != 1:
b+=1
d = pow(b, -1, new_phi)
plaintext = pow(ct, d, new_N)
flag = long_to_bytes(plaintext)
print(flag)
In the code, self.base is incremented by 1 until it is co-prime with self.n.
Since we have both of these values, we can just increment them locally.
$x$ or the obfuscated flag is also incremented with 1 until it is co-prime with $n$, the global variable used to accept input before verifying here:
1
2
3
4
elif x == 2:
n = int(input("Give me the MY modulus : "))
*inp, = input("Enter prime factorization in format [prime1, count1]-[prime2, count2]-[...: ").split('-')
data = []
So what we can do is input a very large $n$ (and let the verification fail since it cannot be called twice), such that it is co-prime with $x$ by default. This is something I figured out after the CTF was over and I did not implement this in my solve script.
Now, we will recover a major chunk of the flag:
1
flag{7h15_fl46_h45_t0_b3_ch4ng3d_du3_t0_3n0u6h_45_53cur17y_3c3p7_3v4l_wh1ch_1s_v3ry_l4rg3_50_1_m4k3_17_b1663r_7h4n_1024_b175_y33333_15_17_r34lly_\x91\xca\xf1\xf7\xff\x18\x8a\x0e}\x03\x93\xf1e"
The last 13 (not 12 because of the carry over bits from addition) bytes are obfuscated.
Solving the subset sum problem
We need to model this problem efficiently so that lattice reduction completes in a reasonable amount of time.
Since we are working with 96 bit keys, we can model this as a modular subset sum problem modulo $2^{96}$.
We have already discussed about how we need 84 keys to solve the subset sum problem, we can also subtract off the keys from the indices 0 to 6 in the sum (since we already removed the 7th index which corresponds to the msb of }).
This leaves us with 77 keys.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
keys = [....]
flag = b"flag{..." #obfuscated
m = bytes_to_long(flag)
suma = m%(2**96)
a = bin(125)[2:].zfill(8)[::-1]
for i in range(8):
if int(a[i]):
suma -= keys[i]
keys = keys[8:] # remove }
for i in range(keys.count(0)):
keys.remove(0)
assert len(keys)==77
res = subset_sum(keys, suma-2, modulus=2**96)
print(res)
I am subtracting my sum by 2 because that’s much $x$ was incremented to make it coprime with $n$.
I tweaked the subset_sum solver code to use BKZ with a block size of 45, which is necessary to get a valid solution.
1
2
3
4
[subset_sum] Density: 0.8021
[subset_sum] Lattice dimensions: (79, 79)
[subset_sum] Lattice reduction took 152.616s
[0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0]
This vector corresponds to the last 96 bits of the flag without the bits of } and without all of the msb bits of each byte.
1
2
a = "".join(map(str, res))[::-1]
flag_last = "".join([chr(int(a[i:i+7],2)) for i in range(0, len(a),7)])
1
'33d3d_t0_d0'
The $13^{th}$ byte still remains a mystery, but given the context, it is easy to guess that it is n.
A proper way to derive it would be to add up all the used keys (without modulo), right shift by 96, then subtract it from the 13th obfuscated byte. It will be n.
Flag
1
flag{th15_fl46_h45_t0_b3_ch4ng3d_du3_t0_3n0u6h_45_53cur17y_3c3p7_3v4l_wh1ch_1s_v3ry_l4rg3_50_1_m4k3_17_b1663r_7h4n_1024_b175_y33333_15_17_r34lly_n33d3d_t0_d0}
Final Thoughts
This was an incredibly layered challenge. I did have a lot of mini-epiphany moments throughout the course of solving this challenge with my team. It is also probably the most time I’ve spent in any challenge in any CTF (Which was fun)
Solve script
solve.sage
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime
from sage.all import ZZ, gcd, matrix, prod, var
from pwn import remote, context
from Crypto.Cipher import AES
from Crypto.Hash import CMAC
from math import gcd
from pwn import xor
import operator
import math
MOD_BITS = 2048 - (1024 // 250) # = 2044
MOD = 1 << MOD_BITS
def derive_cmac_subkey(key):
cipher = AES.new(key, AES.MODE_ECB)
zero_block = b'\x00' * 16
L = cipher.encrypt(zero_block)
def msb(val):
return val[0] & 0x80
def left_shift_xor(val):
shifted = bytearray(val)
carry = 0
for i in range(15, -1, -1):
new_carry = (shifted[i] & 0x80) >> 7
shifted[i] = ((shifted[i] << 1) | carry) & 0xFF
carry = new_carry
if msb(val):
shifted[-1] ^^= 0x87
return bytes(shifted)
K1 = left_shift_xor(L)
return K1
def make_ciphertext(x):
cipher = AES.new(x[:16], AES.MODE_ECB)
ct = b"\x00"*16
K1 = derive_cmac_subkey(x[:16])
cts = []
for i in range((len(x)//16)-1):
pt = x[i*16:(i+1)*16]
ct = cipher.encrypt(xor(pt, ct))
cts.append(ct)
f = xor(ct, K1, x[-16:])
cts.append(f)
return cts
def make_mac(x):
cc = CMAC.new(x[:16], ciphermod=AES)
mac = cc.update(x).hexdigest()
return mac
def generator():
chunk = 128
security = 1024
while 1:
data = []
n = 1
for i in range(2 * security // chunk):
data.append([getPrime(chunk), 1])
n *= data[-1][0]
data.append([2, 2 * security - n.bit_length()])
while n.bit_length() < 2 * security:
n *= 2
if n.bit_length() == 2 * security:
return n, data
def recover_base_candidates(sig: int, *, security_bits=None, want_bits=None):
sig = int(sig)
# Case 1: no wrap-around => exact square
if 0 <= sig < MOD:
b = math.isqrt(sig)
if b * b == sig:
return [b]
# Case 2: wrap-around => modular square roots
roots = _sqrt_mod_2k_all_odd(sig, MOD_BITS)
if not roots:
return []
# We know base ≡ r (mod 2^2044). If base is larger, base = r + t*2^2044.
# If you know/assume a bit-length, you can bound t.
if want_bits is None and security_bits is not None:
# base = p*q with p,q in [2^(s-1), 2^s) => base in [2^(2s-2), 2^(2s))
want_bits = 2 * int(security_bits) # rough "target"; used only for filtering below
candidates = []
if want_bits is None:
# Only return residues mod 2^2044 (what is actually determined)
return roots
lo = 1 << (want_bits - 1)
hi = (1 << want_bits) - 1
for r in roots:
# t must satisfy lo <= r + t*MOD <= hi
t_min = max(0, (lo - r + MOD - 1) // MOD)
t_max = (hi - r) // MOD
for t in range(t_min, t_max + 1):
candidates.append(r + t * MOD)
return sorted(set(candidates))
def phi(data):
b=1
for p,e in data:
b*=(p**(e-1))*(p-1)
return b
def ff(N):
return list(factor(N))
def phi_with_factorization(data):
"""
Compute Euler's totient and return both the value and factorizations
needed for recursive calls.
Args:
data: List of (prime, exponent) pairs
Returns:
result: The phi value
_data: Factorization of the phi value for next recursive call
"""
result = 1
next_factors = []
for p, e in data:
# phi contribution: p^(e-1) * (p-1)
phi_p = (p - 1)
# Add p^(e-1) to result if e > 1
if e > 1:
result *= p ** (e - 1)
next_factors.append((p, e - 1))
# Factor (p-1) using ff() and add to next_factors
factors_p_minus_1 = ff(phi_p)
for prime, exp in factors_p_minus_1:
# Merge with existing factors
found = False
for i, (existing_p, existing_e) in enumerate(next_factors):
if existing_p == prime:
next_factors[i] = (prime, existing_e + exp)
found = True
break
if not found:
next_factors.append((prime, exp))
result *= phi_p
return result, next_factors
def power_tower_mod(a, data, n):
"""
Optimized power tower computation: a↑↑n mod m
Uses cached factorizations to avoid repeated euler_phi calls.
Args:
a: Base
data: List of (prime, exponent) pairs for modulus m
n: Tower height
Returns:
a↑↑n mod m
"""
# Compute m from factorization
m = 1
for p, e in data:
m *= p ** e
# Base case
if n == 1:
return a % m
# Compute phi and get factorization for next level
phi_val, phi_factors = phi_with_factorization(data)
# Recursive call with factorization
exp = power_tower_mod(a, phi_factors, n - 1)
return pow(a, int(exp), int(m))
def subset_sum(weights, targets, modulus=None, N=None, lattice_reduction=None, verbose=False):
"""
Returns the solution of the subset sum problem with the given ``weights``
and ``targets``. Supports multiple knapsacks as well as the modular case
with the ``modulus`` argument. The implementation follows the algorithm
as described in [1].
REFERENCES:
[1] Yanbin Pan and Feng Zhang. *Solving low-density multiple subset sum problems with SVP oracle.*
In Journal of Systems Science and Complexity, p. 228--242. Springer, 2016.
https://link.springer.com/article/10.1007/s11424-015-3324-9
"""
verbose = (lambda *a: print('[subset_sum]', *a)) if verbose else lambda *_: None
if type(weights[0]) is list:
k = len(weights)
n = len(weights[0])
else:
k = 1
n = len(weights)
weights = [weights]
targets = [targets]
if modulus is not None:
density = n / (k * log(modulus, 2))
else:
density = n / (k * log(max(flatten(weights)), 2))
verbose('Density:', round(density.n(), 4))
N = N or ceil(sqrt((n+1)/4))
B = 2 * Matrix.identity(n)
B = B.augment(vector([0] * n))
for j in range(k):
B = B.augment(vector([N * a for a in weights[j]]))
if modulus is not None:
B = B.stack(Matrix.zero(k, n + 1).augment(N * modulus * Matrix.identity(k)))
B = B.stack(vector([1] * (n + 1) + [N * s for s in targets]))
verbose('Lattice dimensions:', B.dimensions())
lattice_reduction_timer = cputime()
if lattice_reduction:
B = lattice_reduction(B)
else:
B = B.LLL()
verbose(f'Lattice reduction took {cputime(lattice_reduction_timer):.3f}s')
for row in B:
if row[n] < 0:
sol = [(x + 1)//2 for x in row[:n]]
else:
sol = [(1 - x)//2 for x in row[:n]]
if any(x not in [0, 1] for x in sol):
continue
for j in range(k):
t = sum(e * a for e, a in zip(sol, weights[j]))
tj = targets[j]
if modulus > 0:
t %= modulus
tj %= modulus
if t != tj:
break
else:
return sol
return None
def _sqrt_mod_2k_all_odd(a: int, k: int):
"""
All solutions to x^2 ≡ a (mod 2^k) for odd a and k>=3.
Exists iff a ≡ 1 (mod 8). Returns 4 roots when they exist.
"""
if k < 3:
raise ValueError("k must be >= 3 for this helper")
a &= (1 << k) - 1
if (a & 1) == 0:
return [] # not needed for this challenge (base is odd)
if (a & 7) != 1:
return [] # no roots for odd a unless a ≡ 1 mod 8
# One root via Hensel lifting starting from r ≡ 1 (mod 8)
r = 1
for i in range(3, k): # lift solution from mod 2^i to mod 2^(i+1)
b = ((a - r * r) >> i) & 1
r += b << (i - 1)
m = 1 << k
r2 = (-r) % m
half = 1 << (k - 1)
return sorted({r % m, r2, (r + half) % m, (r2 + half) % m})
while 1:
io = remote("remote.infoseciitr.in",4001)
io.recvuntil(b"My m4c&ch3353: ")
context.log_level = "DEBUG"
hmac = bytes.fromhex(io.recvline().decode().strip())
io.recvuntil(b"My signature: ")
signature = int(io.recvline().decode().strip())
N = 1
for i in range(16):
N *= getPrime(8)
while N.bit_length() < 128:
N *= 2
K1 = derive_cmac_subkey(long_to_bytes(N))
N = long_to_bytes(N)
cipher = AES.new(N, AES.MODE_ECB)
out = xor(cipher.decrypt(hmac), K1)
for i in range(14):
out = cipher.decrypt(out)
out = xor(out, cipher.encrypt(N))
forged = N+out+b"\x00"*16*14
print("forged N")
hmac1 = bytes.fromhex(make_mac(forged))
assert hmac == hmac1
print("Hmac verified!!")
N = bytes_to_long(forged)
facts = list(factor(N))
print("factored N")
for f in facts:
if int(f[0]).bit_length() > 204:
print("factor was too big! restarting")
break
else:
print("factors are appropriate")
break
io.recvuntil(b"Choose: ")
io.sendline(b"2")
io.recvuntil(b'Give me the MY modulus : ')
io.sendline(str(N).encode())
io.recvuntil(b"Enter prime factorization in format [prime1, count1]-[prime2, count2]-[...: ")
payload = ""
for i in range(len(facts)):
payload += "["+str(facts[i][0])+", "+str(facts[i][1])+"]"
if i!=len(facts)-1:
payload += "-"
io.sendline(payload.encode())
io.recvuntil(b"Yayyyyyyyy! big mac got verified! for n = ")
old_N = int(io.recvline().decode().strip())
io.recvuntil(b"Data = ")
old_factors = eval(io.recvline().decode().strip())
old_phi = phi(old_factors)
new_factors = facts
new_phi = phi(new_factors)
new_N = N
keys = [0]*96
print("recovering bases")
first_base = recover_base_candidates(signature, want_bits=2048)
print("done")
i=0
while i<95:
io.recvuntil(b"Choose: ")
io.sendline(b"3")
io.recvuntil(b"Enter your message : ")
if (i+1)%8 == 0:
keys[i] = 0
i += 1
p = 2**i
io.sendline(str(p).encode())
io.recvuntil(b"Here is your obfuscated message : ")
val = int(io.recvline().decode().strip())
keys[i] = val
i+=1
io.recvuntil(b"Choose: ")
io.sendline(b"1")
io.recvuntil(b"Here is your obfuscated c: ")
ct = int(io.recvline().decode().strip())
print(f"{keys = }")
for b in first_base:
b = power_tower_mod(b, old_factors, 200)
b = power_tower_mod(b, old_factors, 200)
b = power_tower_mod(b, new_factors, 200)
while gcd(b, new_N) != 1:
b+=1
try:
d = pow(b, -1, new_phi)
plaintext = pow(ct, d, new_N)
flag = long_to_bytes(plaintext)
print(flag)
if "flag{" in flag:
break
except:
print("no inverse")
m = bytes_to_long(flag)
suma = m%(2**96)
a = bin(125)[2:].zfill(8)[::-1]
for i in range(8):
if int(a[i]):
suma -= keys[i]
nkeys = keys[8:] # remove }
for i in range(nkeys.count(0)):
nkeys.remove(0)
assert len(nkeys) == 77
print("Running subset sum solver.")
res = subset_sum(nkeys, suma-2, modulus=2**96)
a = "".join(map(str, res))[::-1]
flag_last = "".join([chr(int(a[i:i+7],2)) for i in range(0, len(a),7)])
tot = sum(keys[:8]) # adding back the }
for i in range(len(res)):
if res[i]:
tot += nkeys[i]
prev_byte = chr(((m>>96)&0xff) - (tot >> 96)+1) # n
final_flag = flag + prev_byte + flag_last + "}"
print(final_flag)